網易云課堂-R語言數據分析

剔除異常值后求平均值

mean(w,trim=0.1)
trim是剔除頭和尾的數字

有缺失值時求平均

mean(w,na.rm=TRUE)

加權平均數

weighted.mean(x,wt)

計算百分位數

quantile(w)
給出的是各四分位數

給出0,20%，40%,60%,80%,1的值：
quantile(w,probs=seq(0,1,0.2))

四分位差

IQR(data)

計算峰度和偏度

library(timedate)
skewness(),kurtosis()

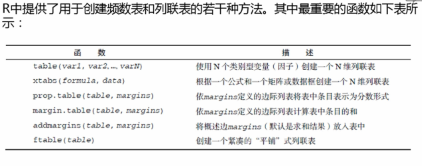
描述性統計

summary()

其他描述性統計包：

library(Hmisc)
describe()

library(pastecs)
stat.desc(x,basic=TRUE,desc=TRUE,norm=FALSE,p=0.95)

分類描述性統計示例：

先根據每省GDP的不同給每省分類(class)，再依此分類對pop,income,gdp進行分類描述性統計

pop<-china[,9]
income<-china[,11]

quantile(gdp)

china[,24]<-rep("n/a",31)
class<-china[,24]
i<-1
while(i<32){
  if (gdp[i]>=920.82) {class[i]=1} 
    if (gdp[i]>=12787) {class[i]=2}
      if (gdp[i]>=17689.93) {class[i]=3}
        if (gdp[i]>=27951.84) {class[i]=4}

  i=i+1
}
china[,24]<-class
re1<-aggregate(income,by=list(class),mean)
re2<-aggregate(pop,by=list(class),mean)
re3<-aggregate(gdp,by=list(class),mean)
result<-data.frame(re1,re2[,2],re3[,2])
names(result)<-c("class","income","pop","gdp")

另一種方法：

mystats<-function(x) c(mean=mean(x),sd=sd(x))
summaryBy(pop+income+gdp~class,data=china,FUN=mystats)

建立頻數表

library(vcd)
mytable<-with(Arthritis,table(class))
轉化成百分比：
prop.table(mytable)
paste(round(prop.table(mytable),2)*100,"%",sep=" ")

列聯表

創建一維列聯表
mytable<-table(A,B)
A是行變量，B是列變量

對行匯總：
margin.table(mytable,1)
對列匯總：
margin.table(mytable,2)

若想要變成百分比：
prop.table(mytable,1)

同時對行和列求和：
addmargins(mytable)
addmargins(prop.table(mytable))

相關性

cor()
偏相關：pcor(c(x1,x2,...),cov(數據))
              前面兩個是要計算偏相關性的兩個變量

相關係數的檢驗：cor.test()
或：
library(psych)
corr.test()

時間序列

#时间序列
SP500<-read.csv("table.csv")
date<-SP500[,1]
close<-SP500[,5]
price<-data.frame(date,close)
pricets<-ts(data=close,start=c(1950,1),frequency = 12)
plot.ts(pricets,header="SP500")
plot.ts(pricets,main="S&P500")
#简单移动平均
library(TTR)
simpleMA<-SMA(pricets,n=4)
plot.ts(simpleMA,main="simple moving average")
#加权平均法
weightedMA<-WMA(pricets,n=4,wts=1:4)
plot.ts(weightedMA,main="weighted moving average")
#分析时间序列趋势
component=decompose(pricets,type=c("additive","multiplicative"),filter=NULL)
component$seasonal
plot(component)
#另一种方法分析时间趋势
stl(x=pricets,s.window="periodic")
#简单指数平滑
pricepre=HoltWinters(pricets,gamma=FALSE)
pricepre
pricepre$SSE
#时间序列的预测
library(forecast)
pricepre2=forecast.HoltWinters(pricepre,h=24)
plot(pricepre2)
#计算自相关性
acf(pricets,lag.max = NULL,type=c("correlation","covariance","partial"),plot=TRUE,na.action = na.fail,demean=TRUE)
#Ljung-Box检验(检验残差序列是否自相关，P值足够小则为自相关，序列不是平稳的)
Box.test(pricets,lag=1,type=c("Box-Pierce","Ljung-Box"),fitdf=0)
#用holt指数预测：
pricepre=HoltWinters(pricets,gamma=FALSE)
plot(pricepre)
pricepre2=forecast.HoltWinters(pricepre,h=24)
plot(pricepre2)
acf(pricepre2$residuals,lag.max = 10)
Box.test(pricepre2$residuals,lag=10,type="Ljung-Box")
#用winter指数法
pricepre=HoltWinters(pricets)
plot(pricepre)
pricepre2=forecast.HoltWinters(pricepre,h=24)
plot(pricepre2)
acf(pricepre2$residuals,lag.max = 10)
Box.test(pricepre2$residuals,lag=10,type="Ljung-Box")

#ARIMA函数
##平稳化处理
baidu<-read.csv("baidu.csv")
bprice<-baidu[,5]
BD<-ts(bprice,frequency = 365, start = c(2009,1,1))
plot.ts(BD)
bddiff<-diff(log(BD))
plot(bddiff)
acf(bddiff,lag.max = 10)
Box.test(bddiff,lag=1,type=c("Box-Pierce","Ljung-Box"),fitdf=0)
##建模
pacf(bddiff,lag.max = 10)
library(forecast)
auto.arima(bddiff,ic="aic")
###假设结果是ARMA(1，1)
##参数估计
pricearima=arima(BD,order=c(1,1,1))
##模型预测
pricepred<-forecast.Arima(pricearima,h=30)
plot.forecast(pricepred)
##诊断残差序列是否为白噪声
acf(pricepred$residuals,lag.max = 5)
Box.test(pricepred$residuals,lag=5,type=c("Ljung-Box"))

判別分析

#判别分析(用china那个表)
##距离判别法
###先计算各点的马氏距离
china<-read.csv("cluster.csv")
varas<-data.frame(china[,2],china[,3])
colm<-colMeans(varas)
sx<-cov(varas)
distance<-mahalanobis(varas,colm,sx)
options(digits=3)
library(WMDB)
G=china$X
G=as.factor(G)
wmd(varas,G)
###开始判断城市等级，根据城市的铁路客运数和GDP
test<-read.csv("ctest.csv")
TEST<-data.frame(test$铁路,test$GDP)
wmd(varas,G,TstX = TEST)

##Fisher判别法
library(MASS)
varas$class=G
names(varas)<-c("rail","eco","class")
detach(varas)
attach(varas)
names(varas)
###准备好数据之后开始做判别分析
varasida<-lda(class~rail+eco)
varasida
plot(varasida)
###开始预测
detach(varas)
rail=c(TEST$test.铁路,rep(0,24))
eco=c(TEST$test.GDP,rep(0,24))
a=data.frame(rail,eco)
predict(varaslda,newdata=a)

##贝叶斯判别法
library(WMDB)
btest<-data.frame(varas$rail,varas$eco)
dbayes(btest,G)

聚类分析

clu<-varas[,-3]
d<-dist(clu)
hc1=hclust(d,method="ward") #离差平方和法
hc2=hclust(d,method="single") #最短距离法
hc3=hclust(d,method="complete") #最长距离法
hc4=hclust(d,method="median") #中间距离法
opar=par(mfrow=c(2,2))
plot(hc1,hang=-1);plot(hc2,hang=-1);plot(hc3,hang=-1);plot(hc4,hang=-1)
par(opar)
##分成3类：
cutree(hc1,4)
china$class=cutree(hc1,4)
##观看分析谱系图
pichc=as.dendrogram(hc1)
par(mfrow=c(1,2))
plot(pichc,type="triangle",nodePar=list(pch=c(1,NA),lab.cex=0.8))
plot(pichc,nodePar=list(pch=2:1),cex=0.4*2:1,horiz=TRUE)

典型相关性分析

el<-read.csv("china.csv")
ell<-data.frame(el$GDP,el$renjun,el$人口,el$居民可支配收入,el$移民倾向指数,el$翻墙倾向指数,el$境外社交网站使用指数,el$政治搜索指数)
###对数据做正态标准离差化
ell<-scale(ell)
ca<-cancor(ell[,1:4],ell[,5:8])
options(digits = 4)
ca

对应分析表

ch=data.frame(A=c(47,22,10),B=c(31,32,11),C=c(2,21,25),D=c(1,10,20))
rownames(ch)=c("purechinese","semichinese","pureenglish")
library(MASS)
ch.ca=corresp(ch,nf=2)
options(digits=4)
ch.ca
biplot(ch.ca)

brand=data.frame(low=c(2,49,4,4,15,1),medium=c(7,7,5,49,2,7),high=c(16,3,23,5,5,14))
rownames(brand)=c("a","b","c","d","e","f")
library(ca)
options(digits=3)
brand.ca=ca(brand)
brand.ca
plot(brand.ca)

主成分分析

ellpr<-princomp(ell[,1:4],cor=TRUE)
options(digits=4)
summary(ellpr,loadings=TRUE)
screeplot(ellpr,type="line",main="碎石图")

因子分析

factest<-data.frame(ell$el.移民倾向指数,ell$el.翻墙倾向指数,ell$el.境外社交网站使用指数,ell$el.政治搜索指数)
factanal(factest,factors=1)

一元线性回归

gdp=ell$el.GDP
pop=ell$el.人口
lmdata=data.frame(gdp,pop)
detach(lmdata)
attach(lmdata)
lm=lm(formula=gdp~pop)
summary(lm)
res=residuals(lm)
plot(res)
par(mfrow=c(2,2))
plot(lm)
###↑可以根据这个图判断有哪些异常值，可将异常值删掉重新回归
detach(lmdata)
pop=c(100,5000,10000,rep(0,28))
a=data.frame(testn)
lmpre=predict(lm,newdata=a,interval="prediction",level=0.95)
lmpre

多元线性回归

mulm=data.frame(ell$el.GDP,ell$el.移民倾向指数,ell$el.翻墙倾向指数,ell$el.境外社交网站使用指数,ell$el.政治搜索指数)
names(mulm)=c("gdp","imm","gfw","web","plt")
detach(mulm)
attach(mulm)
lm.mulm=lm(gdp~imm+gfw+web+plt,data=mulm)
summary(lm.mulm)
##逐步回归
lm.step=step(lm.mulm)
summary(lm.step)

回归诊断

##残差诊断
lm.res=lm.mulm$residuals
lm.fit=predict(lm.mulm)
plot(lm.res~lm.fit,main="残差图")
shapiro.test(lm.res)
##标准残差
rstandard(lm.mulm)
sd=sqrt(deviance(lm.mulm)/df.residual(lm.mulm))
##学生残差
rstudent(lm.mulm)

发现对回归结果比较大的点

##计算leverage并判断
le=hatvalues(lm.mulm)
p=4
n=31
le>(2*(p+1)/n)
##DFFITS统计点
dff=dffits(lm.mulm)
dff>(2*sqrt((p+1)/n))
##cook's距离
cook=cooks.distance(lm.mulm)
cook>4/n
##一个对异常值检测的汇总结果
options(digits=3)
influence.measures(lm.mulm)

多重共线性诊断

options(digits=3)
xx=cor(ell[,2:5]) #提取设计矩阵并标准化
eigen(xx) #求特征根和特征向量
kappa(xx)
library(DAAG)
vif(lm.mulm,digits=3)

岭回归

ling=data.frame(ell$el.GDP,ell$el.renjun,ell$el.人口,ell$el.居民可支配收入)
names(ling)=c("gdp","renjun","pop","income")
detach(ling)
attach(ling)
xx=cor(ell)
kappa(xx)
library(MASS)
plot(lm.ridge(gdp~renjun+pop+income,lambda = seq(0,0.5,0.001)))
select(lm.ridge(gdp~renjun+pop+income,lambda = seq(0,0.5,0.001)))
options(digits = 3)
lm.ridge(gdp~renjun+pop+income,lambda = 0.353)

泊松回归

dat=data.frame(y=c(42,37,10,101,73,14),n=c(500,1200,100,400,500,300),type=rep(c('小','中','大'),2),gender=rep(c('男','女'),each=3))
dat$logn=log(dat$n)
dat.glm=glm(y~type+gender,offset = logn,data=dat,family=poisson(link=log))
summary(dat.glm)
dat.pre=predict(dat.glm)
layout(1)
y=c(42,37,10,101,73,14)
x=exp(dat.pre)
plot(y,x,xlab='观测值',ylab='拟合值',main='索赔次数的拟合效果',pch="*")
abline(0,1) #添加截距为0，斜率为1的直线

负二项回归

library(MASS)
detach(dat)
attach(dat)
dat.glmnb=glm.nb(y~type+gender+offset(logn))
summary(dat.glmnb)

logistic回归

life = data.frame(
  X1=c(2.5, 173, 119, 10, 502, 4, 14.4, 2, 40, 6.6,21.4, 2.8, 2.5, 6, 3.5, 62.2, 10.8, 21.6, 2, 3.4,5.1, 2.4, 1.7, 1.1, 12.8, 1.2, 3.5, 39.7, 62.4, 2.4,34.7, 28.4, 0.9, 30.6, 5.8, 6.1, 2.7, 4.7, 128, 35,2, 8.5, 2, 2, 4.3, 244.8, 4, 5.1, 32, 1.4),
  X2=rep(c(0, 2, 0, 2, 0, 2, 0, 2, 0, 2, 0, 2, 0, 2, 0, 2,0, 2, 0, 2, 0, 2, 0),
         c(1, 4, 2, 2, 1, 1, 8, 1, 5, 1, 5, 1, 1, 1, 2, 1,1, 1, 3, 1, 2, 1, 4)),
  X3=rep(c(0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1),
         c(6, 1, 3, 1, 3, 1, 1, 5, 1, 3, 7, 1, 1, 3, 1, 1, 2, 9)),
  Y=rep(c(0,  1,   0,  1), c(15, 10, 15, 10))
)
glm.sol<-glm(Y~X1+X2+X3, family=binomial, data=life)
summary(glm.sol)
##根据模型对某个具体病人做预测，得到其存活一年以上概率
pre<-predict(glm.sol, data.frame(X1=5,X2=2,X3=1))
p<-exp(pre)/(1+exp(pre))
##若要检测模型预测能力，可以利用ROC图来进行观察,首先用原数据代入模型得出预测概率
pre=predict(glm.sol,type='response')
library(ROCR)
m=prediction(pre,life$Y)
plot(performance(m,'tpr','fpr'))
abline(0,1, lty = 8, col = "grey")

单因素方差分析

##先做正态性检验
x1=c(103,101,98,110,105,100,106)
x2=c(113,107,108,116,114,110,115)
x3=c(82,92,84,86,84,90,88)
shapiro.test(x1)
##方差齐性检验
x=c(x1,x2,x3)
account=data.frame(x,A=factor(rep(1:3,each=7)))
bartlett.test(x~A,data=account)
##单因素方差分析
a.aov=aov(x~A,data=account)
summary(a.aov)
plot(account$x~account$A)
##方差分析的另一种方法
anova(lm(x~A,data=account))

多重t检验

attach(account)
pairwise.t.test(x,A,p.adjust.method = "bonferroni")

Kruskal-Wallis秩和检验

kruskal.test(x~A,data=account)

Kruskal-Wallis秩和检验

kruskal.test(x~A,data=account)

双因素方差

x=c(20,12,20,10,14,22,10,20,12,6,24,14,18,18,10,16,4,8,6,18,26,22,16,20,10)
##生成因子水平
A=gl(5,5)
B=gl(5,1,25)
sales=data.frame(x,A,B)
##方差齐性检验
bartlett.test(x~A,data=sales)
bartlett.test(x~B,data=sales)
##双因素方差分析
sales.aov=aov(x~A+B,data=sales)
summary(sales.aov)

有交互作用的方差分析

time=c(25,24,27,25,25,19,20,23,22,21,29,28,31,28,30,20,17,22,21,17,18,17,13,16,12,22,18,24,21,22)
a=gl(2,15,30)
b=gl(3,5,30,labels=c("一","二","三"))
traffic=data.frame(time,a,b)
bartlett.test(time~a,data=traffic)
op=par(mfrow=c(1,2))
plot(time~a+b,data=traffic)
##绘制交互效应图
attach(traffic)
interaction.plot(a,b,time,legend=F)
interaction.plot(b,a,time,legend=F)
##方差分析
traf.aov=aov(time~a*b,data=traffic)
summary(traf.aov)

协方差分析

weightin=c(15,13,11,12,12,16,14,17,17,16,18,18,21,22,19,18,22,24,20,23,25,27,30,32)
weightic=c(85,83,65,76,80,91,84,90,97,90,100,95,103,106,99,94,89,91,83,95,100,102,105,110)
feed=gl(3,8,24)
data_feed=data.frame(weightin,weightic,feed)
library(HH)
m=ancova(weightic~weightin+feed,data=data_feed)
m

###另一个例子
input <- mtcars[,c("am","mpg","hp")]
print(head(input))
# Get the dataset.
input <- mtcars

# Create the regression model.
result <- aov(mpg~hp*am,data=input)
print(summary(result))
#这一结果表明，这两种马力和传输类型对每加仑英里显著效果，在这两种情况下p的值小于0.05。但是这两个变量之间的相互作用是不显著的，p值大于0.05。
# Create the regression model.
result <- aov(mpg~hp+am,data=input)
print(summary(result))
#这一结果表明，这两种马力和传输类型对每加仑英里显著效果，在这两种情况下p的值小于0.05。
#现在，我们可以比较两个模型得出结论，如果变量之间的相互作用是真的 - 明显。对于这一点，我们使用方差分析 anova()函数。
# Get the dataset.
input <- mtcars
# Create the regression models.
result1 <- aov(mpg~hp*am,data=input)
result2 <- aov(mpg~hp+am,data=input)
# Compare the two models.
print(anova(result1,result2))
#如p值大于0.05，我们得出结论，马力和透射型之间的相互作用是不显著。所以每加仑里程将取决于在汽车中自动和手动变速模式的马力

假设验证

##均值验证,方差已知
bj=c(102.5,102.4,102,101.8,102.1,102.3,102.5,102.6,102.8,103.4,104.2)
library(BSDA)
z.test(x=bj,mu=102.4,sigma.x=0.67,alternative="two.sided")
##均值验证，方差未知
t.test(x=bj,mu=102.4)
##方差检验，均值已知
chisq.var.test=function(x,var,mu=Inf,alternative="two.sided"){
  n=length(x)
  df=n-1
  v=var(x)
  #总体均值已知的情况
  if(mu<Inf){df=n;v=sum((x-mu)^2/n)}
  chi2=df*v/var
  options(digits=4)
  result=list()#产生存放结果的列表
  result$df=df
  result$var=v
  result$chi2=chi2
  result$P=2*min(pchisq(chi2,df),pchisq(chi2,df,lower.tail = F))
  #若是单侧检验
  if(alternative=="greater") result$P=pchisq(chi2,df,lower.tail = F)
  else if(alternative=="less") result$P=pchisq(chi2,df)
  result
}

假设检验--检验两个总体

#检验两总体的均值相同，方差已知(函数)
z.test2=function(x,y,sigma1,sigma2,alternative="two.sided"){
  n1=length(x);n2=length(y)
  result=list()
  mean=mean(x)-mean(y)
  z=mean/sqrt(sigma1^2/n1+sigma2^2/n2)
  options(digits = 4)
  result$mean=mean
  result$z=z
  result$P=2*pnorm(abs(z),lower.tail = FALSE)
  if(alternative=="greater") result$P=pnorm(z)
  else if (alternative=="less") result$P=pnorm(z,lower.tail = FALSE)
  result
}

#检验两个总体的均值，方差未知
t.test(a,b,var.equal = FALSE,alternative = "less")

#成对数据的t检验
t.test(x,y,paired = TRUE, alternative = "greater")

#两总体方差的检验
var.test(x,y)

#比率的二项分布检验
binom.test(214,2000,p=0.1)
##判断一个序列是不是正态分布
###先把函数分成不同区间(这个需要先画出直方图再主观判断)
cut=cut(bj,breaks=c(101.4,101.9,102.4,102.9,104.5))
###计算每个区间的频数
a=table(cut)
###计算原假设条件下数据落入各区间的理论值（br这个区间是平均分的）
br=c(101.5,102,102.5,103,104.5)
p=pnorm(br,mean(bj),sd(bj))
p=c(p[1],p[2]-p[1],p[3]-p[2],1-p[3])
options(digits = 2)
p
###Pearson拟合优度
chisq.test(a,p=p)

#KS分布
##检验一个样本是否符合指数分布
ks.test(x,"prexp",1/1500)
##检验两个样本的分布是否相同
ks.test(x,y)

矩估计

##泊松分布估计lambda
num=c(rep(0:5,c(1532,581,179,41,10,4)))
lambda=mean(num)
lambda
##比较估计值和实际值
k=0:5
ppois=dpois(k,lambda)
###由泊松分布生成的损失次数
poisnum=ppois*length(num)
plot(k,poisnum,ylim=c(0,1600))
samplenum=as.vector(table(num))
points(k,samplenum,type="p",col=2)
legend(4,1000,legend = c("num","poisson"),col=1:2,pch="o")

#多个参数的矩估计（分布为均匀分布,）
library(rootSolve)
x=c(4,5,4,3,9,9,5,7,9,8,0,3,8,0,8,7,2,1,1,2)
m1=mean(x)
m2=var(x)
model=function(x,m1,m2){
  c(f1=x[1]+x[2]-2*m1,
    f2=(x[2]-x[1])^2/12-m2)
}
multiroot(f=model,start=c(0,10),m1=m1,m2=m2)

最大似然估计(用R模拟双峰函数)

library(MASS)
head(geyser,5)
attach(geyser)
hist(waiting,freq=FALSE)
ll=function(para){
  f1=dnorm(waiting,para[2],para[3])
  f2=dnorm(waiting,para[4],para[5])
  f=para[1]*f1+(1-para[1])*f2
  ll=sum(log(f))
  return(-ll)
}

nlminb是计算函数最小值的

geyser.est=nlminb(c(0.5,50,10,80,10),ll,lower=c(0.0001,-Inf,0.0001,-Inf,0.0001),upper=c(0.9999,Inf,Inf,Inf,Inf))
options(digits = 3)
geyser.est$par

p=geyser.est$par[1]
mu1=geyser.est$par[2]
mu2=geyser.est$par[4]
sigma1=geyser.est$par[3]
sigma2=geyser.est$par[5]
x=seq(40,120)

f=p*dnorm(x,mu1,sigma1)+(1-p)*dnorm(x,mu2,sigma2)
hist(waiting,freq = F)
lines(x,f)

用maxLik()函数计算(负二项分布的极大似然估计)

#用maxLik()函数计算(负二项分布的极大似然估计)
num=c(rep(0:5,c(1532,581,179,41,10,4)))
library(maxLik)
loglik=function(para){
  f=dnbinom(num,para[1],1/(1+para[2]))
  ll=sum(log(f))
  return(ll)
}
para=maxLik(loglik,start=c(0.5,0.4))$estimate
r=para[1]
beta=para[2]
#观察检验的一致性
l=length(num)
nbinomnum=dnbinom(0:5,r,1/(1+beta))*l;nbinomnum
plot(0:5,nbinomnum,ylim=c(0,1600))
points(0:5,nbinomnum,type="p",col=2)

单正态总体的区间估计

##均值估计，方差已知
set.seed(111)
x=rnorm(20,10,2)
library("BSDA")
z.test(x,sigma.x = 2)$conf.int
##均值估计，方差未知（函数）
t.test(x)$conf.int

#方差的区间估计
##均值已知
var.conf.int=function(x,mu=Inf,alpha){
  n=length(x)
  if(mu<Inf){
    s2=sum((x-mu)^2)/n
  df=n
  }
  else{
    s2=var(x)
    df=n-1
  }
  c(df*s2/qchisq(1-alpha/2,df),df*s2/qchisq(alpha/2,df))
  }

var.conf.int(x,alpha = 0.05)

两正态总体的区间估计

library(DBSA)
z.test(x,y,sigma.x = ,sigma.y = )$conf.int
##均值差的区间估计(两方差未知但相等)
t.test(x,y,var.equal = TRUE)$conf.int
##均值差的区间估计(两方差未知但不等)(函数)
twosample.ci2=function(x,y,alpha){
  n1=length(x);n2=length(y)
  xbar=mean(x)-mean(y)
  s1=var(x);s2=var(y)
  nu=(s1/n1+s2/n2)^2/(s1^2/n1^2/(n1-1)+s2^2/n2^2/(n2-1))
  z=qt(1-alpha/2,nu)*sqrt(s1/n1+s2/n2)
  c(xbar-z,xbar+z)
}

#两方差比的区间估计
var.test(x,y)$conf.int

#比率的区间估计
prop.test(x,n)
binom.test(x,n,p=0.5,alternative = c("two.sided","less","greater"),conf.level = 0.95)

画图

#多组数据画图
group=read.csv("baiduprice.csv")
group=group[,-1]
summary(group)
##散点图
attach(group)
plot(close2~close1,xlab="close2",ylab="close1")
lines(lowess(close1,close2),col="red",lwd=2)
##等高线图
library(MASS)
a=kde2d(close1,close2)
contour(a,col="blue",xlab="close1",ylab="close2")
##矩阵散点图
plot(group)
##矩阵图
matplot(group,type="l")
##雷达图
stars(ell)

ggplot2画图示例

library(ggplot2)
car1=read.csv("car1.csv")
attach(car1)
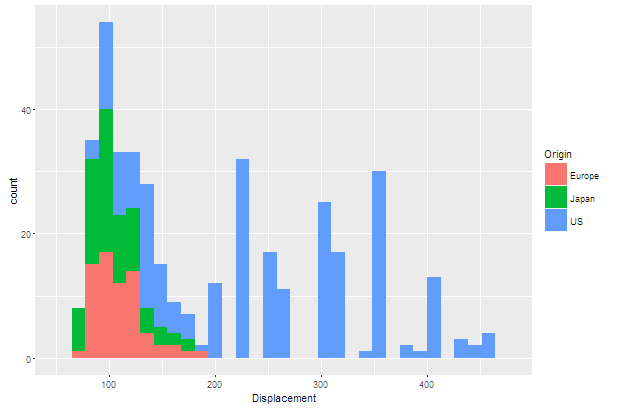
qplot(Displacement,geom="histogram",data=car1,fill=Origin)

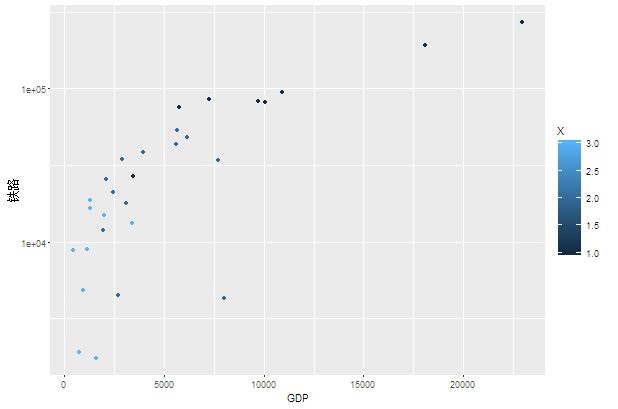
attach(china)
ggplot(china,aes(x=GDP,y=铁路))+geom_point(aes(colour=X))+scale_y_log10()

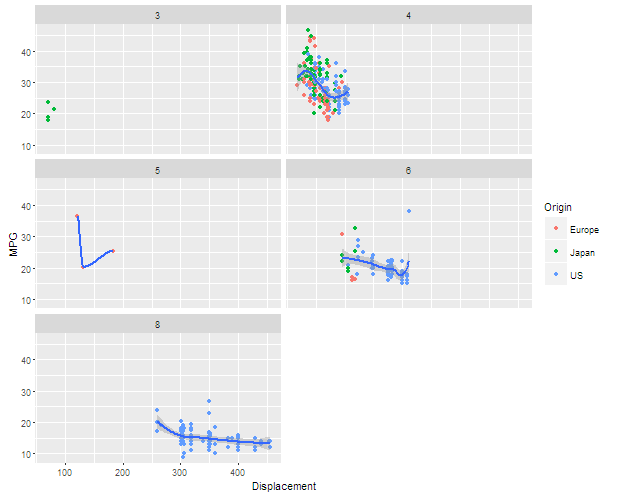
ggplot(car1,aes(x=Displacement,y=MPG))+geom_point(aes(colour=Origin))+geom_smooth()+facet_wrap(~Cylinders,ncol=2)

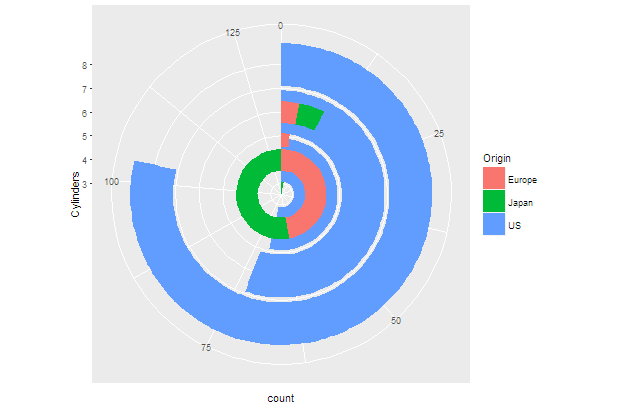
ggplot(car1)+geom_bar(aes(x=Cylinders,fill=Origin))+coord_polar(theta = "y")

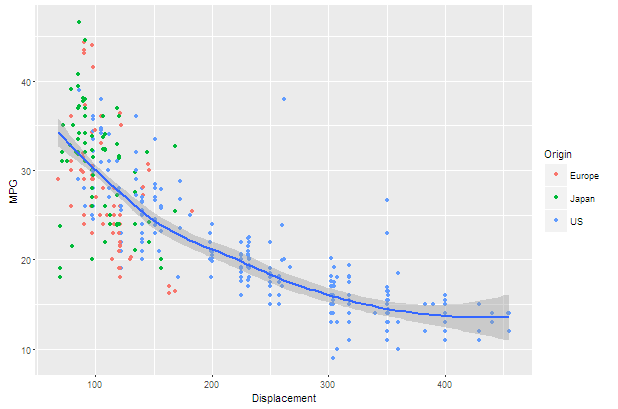
 ggplot(car1,aes(x=Displacement,y=MPG))+geom_point(aes(colour=Origin))+geom_smooth()

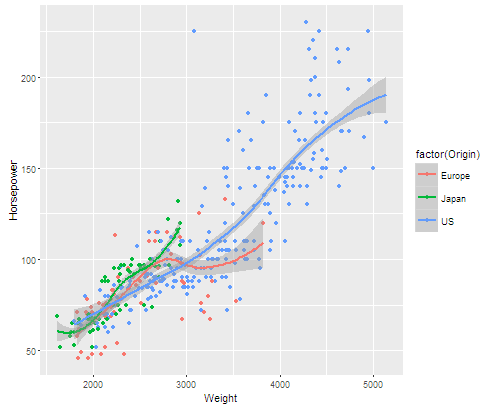
library(reshape2)
longdata=melt(car1,id.vars = c("Origin","Horsepower","Weight"),measure.vars = 2:4)
library(ggplot2)
p=ggplot(data=longdata,aes(x=Weight,y=Horsepower,color=factor(Origin)))
str(longdata)
p+geom_point()+geom_smooth()

退火算法

library(quantmod)
getSymbols(c('IBM','SPY','YHOO'))
IBM_ret=dailyReturn(IBM)
SPY_ret=dailyReturn(SPY)
YHOO_ret=dailyReturn(YHOO)
data=merge(IBM_ret,SPY_ret,YHOO_ret)
library(timeSeries)
library(fPortfolio)
data=as.timeSeries(data)
Frontier=portfolioFrontier(data)
Frontier
plot(Frontier)

K-means聚类分析

china2<-read.csv("china.csv")
rownames(china2)=china2[,1]
chinat=data.frame(china2[,2:4],china2[,7],china2[,9],china2[,10:12])
KM=kmeans(chinat,4)
sort(KM$cluster)

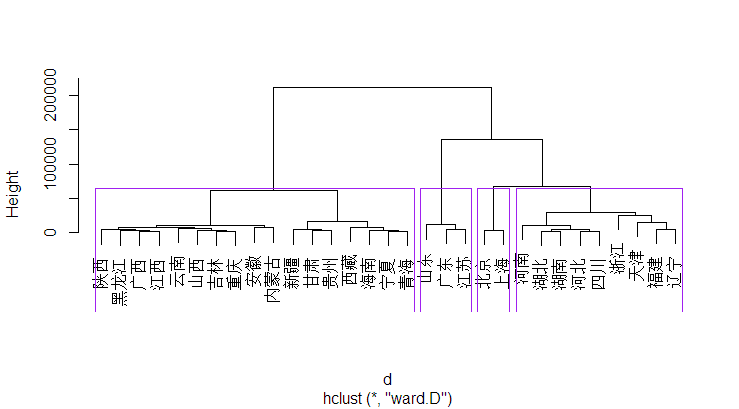
层次聚类分析

d=dist(chinat)
hc=hclust(d,method="ward")
plclust(hc)
rect.hclust(hc,k=4,border="purple")